第 12 课：人脸识别和神经风格转换

（Face recognition & Neural style transfer）

（一）人脸识别

在人脸识别的相关文献中，人们经常提到人脸验证（face verification）和人脸识别 face recognition）。
人脸验证问题： 如果你有一张输入图片，以及某人的ID或者是名字，要做的是验证输入图片是否是这个人。有时候也被称作 1对 1问题。
人脸识别问题： 难度大很多，因为容错率低很多。

同时，一个重大问题是每个人的照片只有一张。如果用softmax单元的输出来对应每个员工，如此小的训练集得到的效果并不好，
同时每新增一个员工，就要调整网络结构和重新训练，明显不可行

因此，下面我们要介绍 一次学习（One-shot learning） 的办法

（1） Similarity函数 和 Siamese 网络

我们要神经网络以两张图片作为输入，然后输出这两张图片的差异值。
也就是要学习 Similarity函数 𝑑(𝑖𝑚𝑔1,𝑖𝑚𝑔2)=𝑑𝑒𝑔𝑟𝑒𝑒 𝑜𝑓 𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑐𝑒 𝑏𝑒𝑡𝑤𝑒𝑒𝑛 𝑖𝑚𝑎𝑔𝑒𝑠，

我们设置一个超参数 τ
𝑑(𝑖𝑚𝑔1,𝑖𝑚𝑔2) < τ，认为两张图片是同一个人，
𝑑(𝑖𝑚𝑔1,𝑖𝑚𝑔2) > τ，认为两张图片是不同的两个人

Similarity函数 的功能具体怎么实现呢？ 可以使用 Siamese网络

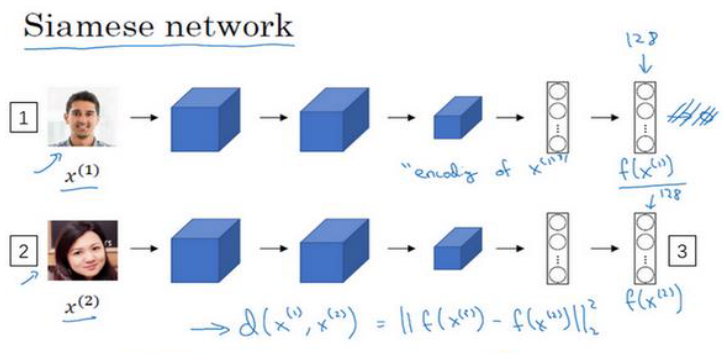
之前我们都是把图像经过一系列处理得到的 特征向量 放入 softmax层 进行分类，但在这里我们不这么做
我们把这个 特征向量 叫做 𝑓(𝑥(1))。你可以把 𝑓(𝑥(1))看作是输入图像 𝑥(1)的编码
把第二张图片输入到 同一个神经网络，得到另一个 特征向量 𝑓(𝑥(2))，这个向量代表第二个图片的编码
这里 𝑥(1)和 𝑥(2)仅仅代表两个输入图片，他们没必要非是第一个和第二个训练样本，可以是任意两个图片。

然后就可以计算d：

$$d(x^{(1)}, x^{(2)}) = \|f(x^{(1)}) - f(x^{(2)})\|_2^2$$

对于两个不同的输入，运行相同的卷积神经网络，然后比较它们，这就是Siamese网络架构。

注意：这两个网络有相同的参数，所以实际要做的就是训练一个网络

那如何训练定义损失函数来训练这个网络呢？ 我们需要用到 三元组损失函数 来计算 损失（ Triplet 损失）, 进而实现梯度下降

我们一般需要比较 3张图片，Anchor图片、 Positive图片和 Negative图片，简写成 𝐴、 𝑃、 𝑁
让 Anchor图片和 Positive图片（ Positive意味着是同一个人）的距离很近，
Anchor图片与 Negative图片（ Negative意味着是非同一个人）的距离很远，

我们最后想要的是网络的参数或者编码能够满足以下特性：

$$d(A,P) + \alpha \leq d(A,N)$$

即

$$d(A,P) - d(A,N) + \alpha \leq 0$$

即

$$\|f(A) - f(P)\|_2^2 -\|f(A) - f(N)\|_2^2 + \alpha \leq 0$$

其中 $\alpha$ 超参数 是防止把所有东西都学成0，出现 0-0 < 0 的无效情况。这个参数也叫 间隔（margin）

接下来就可以得到损失函数了：

$$L(A,P,N) = max( \|f(A) - f(P)\|_2^2 -\|f(A) - f(N)\|_2^2 + \alpha , 0)$$

只要前面一项小于0了，那么损失函数就是0

这是一个三元组定义的损失函数，整个网络的代价函数为：

$$I = \sum_{i=1}^{m} L(A^{(i)},P^{(i)},N^{(i)})$$

假如你有一个 10000个图片的训练集，里面是 1000个不同的人的照片，
你要做的就是取这 10000个图片，然后生成这样的三元组，然后训练你的学习算法，对这种代价函数用梯度下降.

注意：

1. 由于需要成对的 𝐴 和 𝑃，即同一个人的成对的图片，因此对于训练集，你需要确保有同一个人的多个图片
   当然，训练完这个系统之后，你可以应用到你的一次学习问题上，只需要一张照片即可。
2. 如果你从训练集中随机地选择 𝐴、 𝑃和 𝑁，其实 $d(A,P) + \alpha \leq d(A,N)$ 这个条件很好达到，因此网络不能从中学到什么。
   所以要尽可能选择难训练的三元组𝐴、 𝑃和 𝑁。所谓的 “难训练” 是指 d(A,P) 很接近 d(A,N)。

现在的人脸识别系统，尤其是大规模的商业人脸识别系统都是在很大的数据集上训练，这些数据集并不容易获得。
幸运的是，一些公司已经训练了这些大型的网络并且上传了模型参数。
所以一般下载别人的预训练模型，而不是一切都要从头开始。

（2）人脸验证与二分类

除了Triplet loss，还有其他学习参数的方法，比如把人脸识别当成一个二分类问题

如下图，Siamese网络不变，但是把特征向量 输入到逻辑回归单元，如果是相同的人，那么输出是 1，若是不同的人，输出是 0。

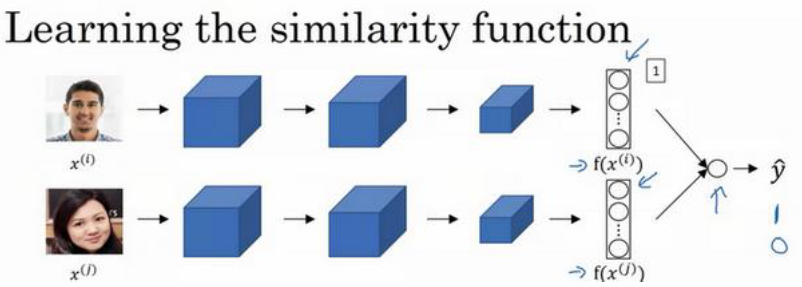
这里的逻辑回归单元具体实现如下：

$$\hat{y} = \sigma\left(\sum_{k=1}^{128} w_{i} |f(x^{(i)})_k - f(x^{(j)})_k| + b\right)$$

其中
$f(x^{(i)})_k$ 代表图片 $x^{(i)}$ 的编码，下标 𝑘代表选择这个向量中的第 𝑘个元素，
$|f(x^{(i)})_k - f(x^{(j)})_k|$ 对这两个编码取元素差的绝对值。这一块可以替换为 $\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k}$ , 这个公式也叫做 $X^2$ 公式, 也被称为 X 平方相似度

最后的逻辑回归增加了参数 𝑤𝑖和 𝑏，就像普通的逻辑回归一样。
与之前类似，你正在训练一个Siamese网络，意味着上面这个神经网络拥有的参数和下面神经网络的相同

注意：

1. 对于一张已经在数据库中的图片，不需要每次都重新计算特征向量，可以先计算好存起来，要比较新照片时就直接拿出来用
2. 和之前不同，这里使用成对图片的训练集， 而不是3个一组。目标标签是 1表示一对图片是一个人，目标标签是 0表示图片中是不同的人。

（二）神经风格迁移

(neural style transfer)

下图所示的就是一个神经风格迁移案例
我们使用 𝐶 来表示内容图像， 𝑆 表示风格图像， 𝐺 表示生成的图像。

在深入了解如何实现神经风格迁移之前，我们先直观地介绍 卷积神经网络不同层之间的具体运算

（1）卷积网络的原理 探究过程

我们之前就了解过，神经网络的浅层专注于局部特征，越深获得的特征越复杂、越完整
这里对这个研究过程进行详细的展开：

在神经网络中，一个“隐藏单元”指的是隐藏层中的一个神经元

查看第一层的输出：

1. 训练网络：首先，你训练了一个如AlexNet这样的卷积神经网络，这是一个深层的网络，通常包含多个卷积层和池化层。
2. 遍历训练集：经过训练后，你通过网络传递整个训练集，监控每一层的输出，以便于分析每个隐藏单元（神经元）的激活情况。
3. 最大化激活的图片块： 对于每一层的每个隐藏单元，你查找那些使得这个单元激活值最大的图片或图片的一部分（图片块）。这些图片块是那些在经过卷积层后，能够在特定神经元产生最强响应的输入区域。
   例如，第一层可能专注于检测边缘、颜色或纹理等简单特征。通过找出哪些图片块最能激活某个单元，可以看出这个单元在学习过程中专门对哪些视觉特征作出响应。
4. 局部响应特性：在网络的早期层（如第一层），每个隐藏单元只能“看到”输入图片的一小部分。这是因为第一层的卷积操作通常只覆盖输入图片的一个小局部区域。
5. 可视化激活：通过选取那些最大化特定单元激活的图片块，你可以可视化这些单元的功能。例如，如果一个单元在被图片中的垂直边缘激活时活跃度最高，那么这表明该单元可能在检测垂直方向的边缘。

然后你可以选一个另一个第一层的隐藏单元，重复刚才的步骤
在更深的层上，你可以重复这个过程。

（2） 神经风格迁移

我们的目标是：给你一个内容图像𝐶 和一个风格图片 𝑆，生成一个新图片 𝐺
然而 𝐺 不是一步就生成的，而是先去 生成一个随机噪点图片，然后给 生成的图像 定义一个代价函数，
通过不断梯度下降来最小化代价函数，从而实现生成图片的逐渐渲染成型

因此我们首先要为生成的图像定义一个代价函数，用来评判某个生成图像的好坏

我们把这个代价函数定义为两个部分
内容代价 $J_{content}(C,G)$ : 度量生成图片 𝐺的内容与内容图片 𝐶 的内容有多相似。
风格代价 $J_{style}(S,G)$ : 度量生成图片 𝐺的风格和风格图片 𝑆 的风格的相似度。

最后：$J(G)=\alpha J_{content}(C,G) + \beta J_{style}(S,G)$

内容代价函数的具体算法：

1. 选择一个中间层 $l$
2. 取 $a^{[l][C]}$ 和 $a^{[l][G]}$，代表这两个图片 𝐶 和 𝐺 的 𝑙 层的激活函数值。如果这两个激活值相似，那么就意味着两个图片的内容相似。
3. 使用定义 (L2范数的平方)：

$$J_{\text{content}}(C, G) = \frac{1}{2} \left\| a^{[l][C]} - a^{[l][G]} \right\|^2$$

注意：
如果 𝑙 是个很小的数，比如用隐含层 1，由于进行了过于底层特征的比较，你的生成图片会过于接近你的内容图片。
如果 𝑙 是个很大的数，由于层数太深，那就会太抽象，比如只会确保生成图片里有一个狗即可，与内容图片差距过大
所以在实际中，通常 𝑙 会选择在网络的中间层，既不太浅也不很深，

风格代价函数的具体算法：

我们首先要搞清楚，什么是 “图片的风格”
在下图中，我们选择了某一层 $l$, 这一层的尺寸为 $n_h \times n_w \times n_c$

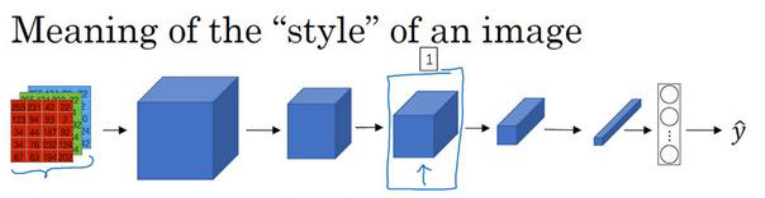
图片的风格 就是 𝑙 层中各个通道之间激活项的相关系数。什么是 不同通道之间激活项的相关系数呢？
为了理解 “激活项的相关系数”，我们把这个激活块的不同通道渲染成不同的颜色。
假如我们有 5个通道，我们将它们染成了五种颜色

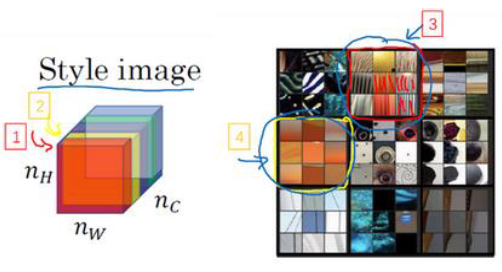
我们知道每个通道对应上一层隐藏层中的一个 过滤器，也就是检测对应的某一个特征
假设上一层输出的左下角是黄色条纹，第一个通道检测的是黄色特征，因此被激活，第二个通道检测的是条纹特征，因此也被激活
换句话说，上一层激活值的左下角在第一个通道中含有某个激活项，同时 第二个通道 在这个位置也含有某个激活项，
如果这幅图片中出现条纹的地方很大概率是黄色的，就认为这两个通道有高度相关性
而相关系数描述的就是当图片某处出现这种条纹时，该处又同时是黄色的可能性。

如果上一层激活值的左下角在第一个通道中含有某个激活项，同时 第二个通道 在这个位置也含有某个激活项，于是它们组成了一对数字
然后我们再看看这个激活项块中其他位置的激活项，它们也分别组成了很多对数字，分别来自各个通道
现在我们得到了很多个数字对，当我们取得这两个 𝑛𝐻×𝑛𝑊 的通道中所有的数字对后，就可以计算它们的相关系数了

计算过程如下：

1. 计算风格矩阵 $G^{[l](S)}$ , 𝑙 表示层数， 𝑆 表示风格图像 。$G^{[l](S)}$ 的尺寸为$n_c^{[l]}\times n_c^{[l]}$

$$G^{[l](S)}_{kk'} = \sum_{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_W^{[l]}} a^{[l](S)}_{i,j,k} a^{[l](S)}_{i,j,k'}$$ $$a_{i,j,k}^{[l]} = 隐藏层 l 中 (i,j,k)位置的激活项 , 𝑖、 𝑗、 𝑘分别代表该位置的高度、宽度以及对应的通道数\\$$

在这个矩阵中 𝑘和 𝑘′元素被用来描述 𝑘通道和 𝑘′通道之间的相关系数。
$G^{[l]}_{kk'}$ 可以用来测量 𝑘 通道与 𝑘′ 通道中的激活项之间的相关系数， 𝑘 和 𝑘′会在 1到 $n_c$之间取值， $n_c$ 就是 𝑙 层中通道的总数量。

2. 同样，我们也对生成的图像进行这个操作

$$G^{[l](G)}_{kk'} = \sum_{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_W^{[l]}} a^{[l](G)}_{i,j,k} a^{[l](G)}_{i,j,k'}$$

上标 (𝑆)和 (𝐺)分别表示在风格图像 S中的激活项和在生成图像 𝐺的激活项。

3. 要注意，如果两个通道中的激活项数值都很大，那么 $G^{[l]}_{kk'}$ 也会很大，对应强相关。反之，不相关，$G^{[l]}_{kk'}$就会很小
4. 现在我们有2个风格矩阵，分别从风格图像 𝑆 和生成图像 𝐺 得到。

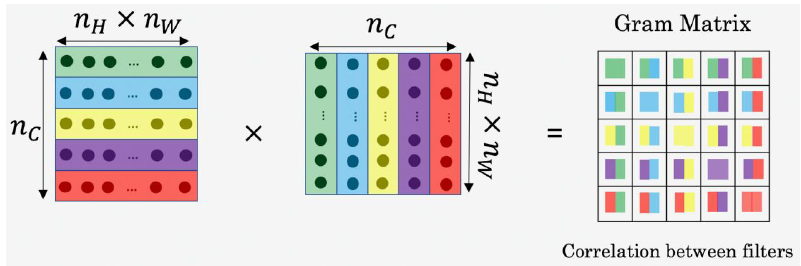
5. 最后，如果我们将𝑆和 𝐺代入到风格代价函数中去计算，

$$J_{\text{style}}(S, G) = \frac{1}{(2n_H^{[l]} n_W^{[l]} n_C^{[l]})^2} \sum_{k} \sum_{k'} \left( G^{[l](S)}_{kk'} - G^{[l](G)}_{kk'} \right)$$

即

$$J_{\text{style}}(S, G) = \frac{1}{\left(2n_H^{[l]} n_W^{[l]} n_C^{[l]}\right)^2} \left\|G^{[l](S)} - G^{[l](G)}\right\|_F^2$$

注意：

1. 我们之所以用大写字母 𝐺来代表这些风格矩阵，是因为在线性代数中这种矩阵有时也叫 Gram矩阵，但在这里我只把它们叫做风格矩阵。
2. 如果你对各层都使用风格代价函数，会让结果变得更好。如果要对各层都使用风格代价函数，你可以把各个层的结果（各层的风格代价函数）都加起来，并对每个层定义权重𝜆[𝑙]，这样将使你能够在神经网络中使用不同的层，使得我们的神经网络在计算风格时能够同时考虑到低级和高级特征的相关数。

算法的整个流程如下：

1. 随机初始化生成图像 𝐺，它可以是任何你想要的尺寸。
2. 梯度下降 来减小代价函数 J(G), 更新 $G := G - \frac{\partial}{\partial G} J(G)$ 。在这个步骤中，你实际上更新的是图像 𝐺的像素值。

（三）1维到3维的推广

我们已经学习了许多关于卷积神经网络（ConvNets）的知识，从卷积神经网络框架，到如何使用它进行图像识别、对象检测、人脸识别与神经网络转换。
即使我们大部分讨论的图像数据都是 2D数据，但许多思想不仅局限于 2D图像，甚至可以延伸至 1D，乃至 3D数据。

一维卷积：

在这种情况下你需要使用一个 1维过滤器 进行卷积，你只需要一个 1×5的过滤器，在不同的位置中应用类似的方法

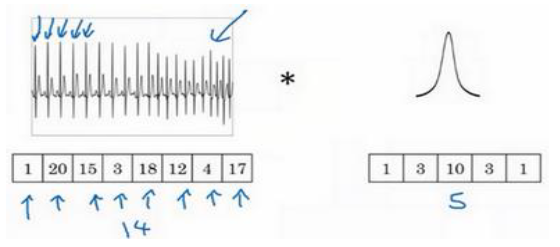
当你对这个1维信号使用卷积，你将发现一个 14维的数据与 5维数据进行卷积，并产生一个 10维输出。
如果你有 16个过滤器，可能你最后会获得一个 10×16的数据，这可能会是你卷积网络中的某一层。

不过对于1D数据而言，我们后面还会学到序列模型（RNN），专门解决这种问题

三维卷积：

比如CT的人体切片。
也要使用 3D 的过滤器进行卷积，原理和上面相同